不知道大家是否见过三角形轮子的自行车。是的，骑起来挺平稳，不会颠簸。

工程师 Sergii Gordieiev 发明的三角车轮自行车丨图源：Youtuber The Q

把一个圆放在两条平行线中间，使之与这两条平行线保持相切。那么无论我们如何转动这个圆，这两条平行线的距离始终不变。我们管这一性质叫定宽性。

然而，圆不是平面上唯一的定宽曲线。若以一个正三角形的三个顶点作为圆心，以边长作为半径，则包裹住正三角形的三段圆弧围成的图形，就是一条非圆定宽曲线。实际上，它是除圆之外最简单和最著名的定宽曲线：Reuleaux 三角形。

因为它的宽度是恒定的，所以 Reuleaux 三角形是“除了圆之外，还可以制作什么形状的井盖”这个问题的一个答案。感兴趣的朋友可以尝试验证一下它的定宽性质。

上面动图里的自行车，其轮胎的形状正是 Reuleaux 三角形。定宽性可使自行车平稳行驶，但由于工程和力学上的现实原因，Reuleaux 三角形的轮胎目前并无实用性。不过，这并不意味着 Reuleaux 三角形仅能充当短视频里的噱头——后文我们会介绍它在工业上的各种应用——它也是数学里重要的研究对象。

但最令人尴尬的一点反而是，历史上对 Reuleaux 三角形和其它定宽曲线研究得越透彻，就愈发彰显我们对三维，以及更高维度欧式空间里的定宽几何体所知的匮乏。

耶路撒冷希伯来大学的数学荣誉教授吉尔·凯莱（Gil Kalai）是当代组合学领域的领导者之一。他十多年前曾在数学社区 MathOverflow 上评论道：“恒定宽度的集合（球除外）没有幸运地被选作 Banach 空间的范数，无法吸引强大的 Banach 空间理论的专家来研究它们在大维度下的渐近特性。”所以，数学界把高维空间定宽几何研究打入了冷宫。但他随后笔锋一转：“但它们（高维定宽几何体）非常令人兴奋，这看起来是一个非常基本的问题。”

此处“非常基本的问题”特指奥德·施拉姆（Oded Schramm，Kalai 教授曾经的学生）于 1988 年在普林斯顿大学读博期间提出的、看似很简单的问题：我们能在任何维度上构造一个比球小指数级的定宽几何体吗？

这个非常基本的问题，困惑了数学界长达 30 多年。直到今年 5 月，5 名研究人员报告说，答案是肯定的。

他们不仅解决了一个高维几何中的难题，而且让数学界第一次看到了这些神秘的高维几何对象可能长什么样子。虽然这些形状很容易定义，但却出奇地神秘。现在，研究人员终于可以进入几何宇宙中曾经完全无法接近的一角。

定义三维空间里的定宽几何对象（后文简称为定宽体）的方式，与前面定义定宽曲线的方式类似。只不过曲线是夹在两条平行线之间，而立体对象要夹在两个平行的平面之间。如果该立体对象无论怎么运动，都不会改变平行平面的距离，那我们就称其为三维定宽体。

类似地，可以定义一般n维空间里的定宽体。只不过要把平面换成 n-1 维的超平面。

三维空间里的球体，n 维空间里半径为 1 的 n 维单位球（记为 Bn），都是最容易想到的定宽体。但是，球是否就是唯一一类定宽体呢？

历史上的数学家也想弄清这个问题。他们仿造前面构造 Reuleaux 三角形的方式，在三维空间里构造了 Reuleaux 四面体。思路就是以正四面体各顶点为圆心，以边长为半径，构造四个球壳。被四个球壳彼此分割的球面包裹住的空间，就是 Reuleaux 四面体。

一开始，人们猜测 Reuleaux 四面体是三维空间里的非球定宽体。但很遗憾，它并不是。大家可以试着计算一下，验证这一点。

Reuleaux 四面体 | 图源：Reuleaux tetrahedron - Wikipedia

好消息是，可以通过局部“手术”，把它改造成定宽体！所以现在我们有了第一种非球形的三维定宽体——Meissner 体。

想必读者朋友也注意到了，在三维空间中构造定宽体已然颇为不易，升至更高维的空间中，难度超乎想象。更何况，为了解答 Schramm 提出的难题，还需要保证：

对某个小于 1 的正数 q，当 n 足够大时，总是存在宽度为 2 的 n 维定宽体 Kn，其体积V（Kn）＜qn·V（Bn）。其中V（*）表示对象*的体积。

数学家想不出如何直接构造出高维定宽体，所以只能依赖既有的经验。仿照二维和三维成功路径，从一组点开始（称之为“种子”），然后以每个种子为圆心作一个高维球面。寻找能被所有球面包裹的对象，看看它是否具有恒定宽度。

但是在高维世界里，要弄清楚种子的子集能带来的形状，是非常困难的工作。

4 位乌克兰的数学家安德烈·阿曼（Andrii Arman）、安德烈·邦达连科（Andriy Bondarenko）、丹尼洛·拉德琴科（Danylo Radchenko）和 安德烈·普里马克（Andriy Primak）对不同的种子进行了实验，最终试出了一条特定曲面。他们知道曲面划出了一个区域，其中包含一个足够小的定宽体。但他们想了解该定宽体到底是什么样子。

在他们追寻答案时，Arman 看到了 MathOverflow 上 2022 年的一则帖子，进而结识了肯特州立大学的 Fedor Nazarov。后者一直在独立研究 Schramm 的问题，他的方法看起来与乌克兰团队的方法非常相似，尽管他也陷入了困境。乌克兰团队邀请他加入他们。就在那时， Nazarov 意识到了其他人错过的东西：他们的种子赋予的形状不单纯是包含了一个定宽体，它本身就是定宽体！

在那个尤里卡时刻，问题全都迎刃而解。他们的工作指出，对任意足够大的维度 n，都存在一个宽度为 2 的定宽体 Kn，满足V（Kn）＜0.9n·V（Bn）。

Arman 说，尽管结论背后有着复杂的思路，但他们的构造是本科生就足以验证的。实际上，他们的论文仅有 7 页（见参考[6]），而且没有给出构造几何体的 3D 图示。在一篇几何学论文里，没有几何对象的图示，甚至引起了很多数学家的吐槽。

卡内基梅隆大学的数字几何学家、计算机科学与机器人学副教授 Keenan Crane 按论文里的方法制作了 3 维定宽体的图像，并特意指出，因为原始论文竟然没有配图，所以自己动手制作了一个。

3 维空间中体积小于球体的定宽体。丨图源：卡内基梅隆大学数字几何学家、计算机科学与机器人学副教授 Keenan Crane

虽然 Arman 等人的工作揭示了一般 n 维空间里定宽体的渐进特性，但目前实质上还处于“皮毛”阶段。和二维定宽曲线相比，我们对高维定宽体的各种细节还知之甚少。

除了之前介绍过的 Reuleaux 三角形，还存在大量的定宽曲线。实际上，我们可以从数学上证明，每一个奇数条边的正多边形都可以借助画圆弧的方法生成一条定宽曲线。此类定宽曲线就叫做 Reuleaux 多边形。Reuleaux 三角形就是其中最简单的 Reuleaux 多边形。

但是，Reuleaux 多边形的边缘都是圆弧，那是否存在边缘不是圆弧的定宽曲线呢？

答案是肯定的。

我们有非圆弧拼接，更加光滑的代数定宽曲线。例如，下面的多项式的零点形成一条宽度恒定的非圆平滑代数曲线：

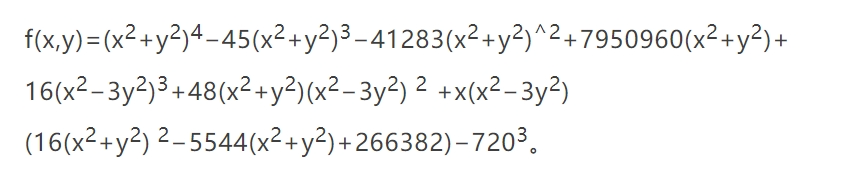
曲线的次数为 8，这是定义定宽非圆曲线的多项式的最小可能次数。

对于所有定宽曲线，有 Barbier 定理：定宽曲线的周长 πw（w就是那个恒定的宽度），无论其形状如何。

此外，非常重要的 Blaschke-Lebesgue 定理指出，Reuleaux 三角形在同宽度的所有定宽曲线中具有最小的面积。很多数学家都想找到三维里体积最小的定宽体，但至今徒劳无功。

Arman 的 5 人团队在解答了 Schramm 问题后，最近几个月里就在研究上面的问题。但因为毫无结果，不久前宣布放弃追逐，回到他们早年的研究工作之中。

我们毕竟是生活在三维世界里，高维几何学的前沿研究往往对现实生活影响有限。根据 Arman 的说法，在更高的维度上，他们发现的定宽体或许有助于开发用于分析高维数据集的机器学习方法。

但是，Reuleaux 三角形则是确凿无疑地早已被应用于各种生活和工业场景中。19 世纪的德国工程师 Franz Reuleaux 是研究将一种运动转换为另一种运动的机械的先驱。他在设计中使用了 Reuleaux 三角形。这就是其名称的由来。但它的历史可追溯得更加久远。

Reuleaux 三角形的早期应用来自达·芬奇于 1514 年左右绘制的世界地图，其中地球的球面被分成八片，每片都被压成一个 Reuleaux 三角形的形状。

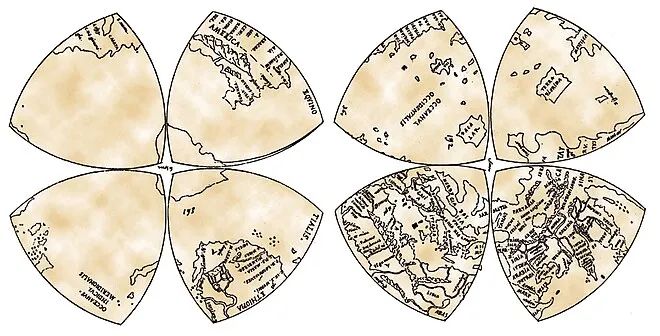
达·芬奇于 1514 年左右绘制的世界地图 | 图源：Reuleaux triangle – Wikipedia

不过第一个意识到定宽曲线的存在、并观察到 Reuleaux 三角形具有定宽性质的人可能是欧拉（Leonhard Euler）。在他于 1771 年发表并于 1781 年重新整理发表的论文中，欧拉研究了曲线三角形以及他称之为类圆的定宽曲线。

Reuleaux 三角形和其它定宽曲线的存在表明，仅靠直径测量无法验证物体是否具有圆形横截面。

1986 年，“挑战者”号航天飞机在升空 73 秒后爆炸，著名物理学家理查德·费曼（Richard Feynman）被请来调查事故原因。他后来证明，本来用于连接航天飞机固体火箭助推器部分的“O 形圈”密封件由于低温而失效，造成了灾难性的后果。但他也发现了不少别的问题。其中就包括 NASA 测量 O 形圈形状的方式。在飞行前测试期间，工程师反复测量了密封件的宽度，以验证它们没有变形。

费曼后来写道，因为存在定宽曲线，这些测量是无用的。

虽然它们给圆截面测量带来了隐患，但定宽曲线的形状也带来了非常有用的性质。目前有几种类型的机械采用 Reuleaux 三角形的形状，基于其能够在正方形内旋转的特性。

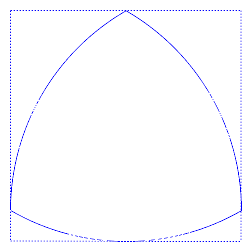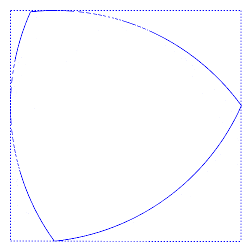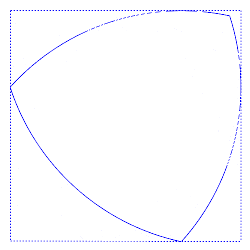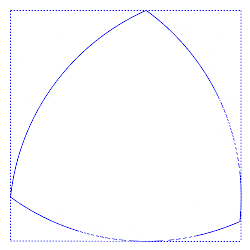
Reuleaux 三角形在一个正方形内滚动，同时始终接触所有四个边。丨图源：Curve of constant width - Wikipedia

Watts Brothers Tool Works 的方形钻头具有 Reuleaux 三角形的形状，经过凹面修饰以形成切割表面。当安装在允许钻头没有固定旋转中心的特殊卡盘中时，它可以钻出一个近乎方形的孔。

德国工程师菲利克斯·汪克尔（Felix Wankel）借助 Reuleaux 三角形设计了一种采用偏心旋转，将压力转化为旋转运动的内燃机。

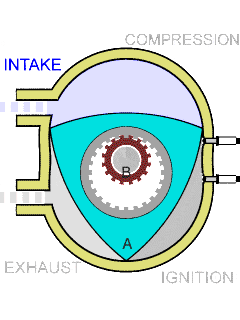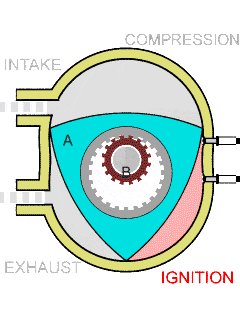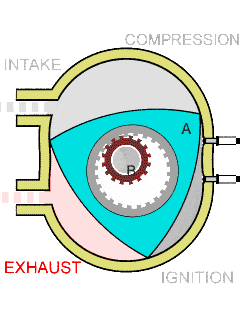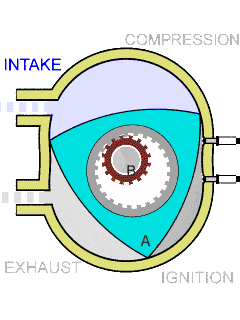
Wankel KKM 发动机的冲程循环丨图源：Wankel engine - Wikipedia

大约 50 年前，马自达的工程师成功地将 Wankel 的转子发动机商业化。转子发动机因其比传统活塞发动机更小、更轻，且具有优越的功率重量比而闻名。与传统发动机不同，转子发动机没有往复运动的部件。它使用一个在壳体内旋转的三角形转子，使其运行更安静、更平稳。这种设计还允许在给定排量下实现出色的性能。

尽管最后一款使用 13B 转子发动机的车型 RX-8在2012 年停产，马自达仍继续生产转子发动机及其零部件，保持着转子发动机的传统。

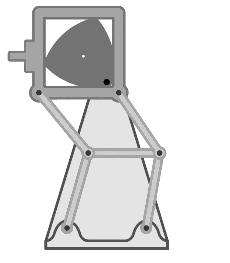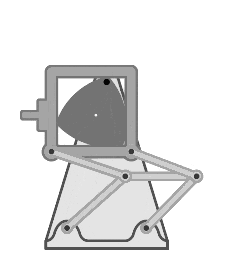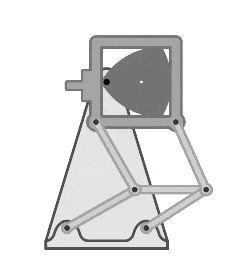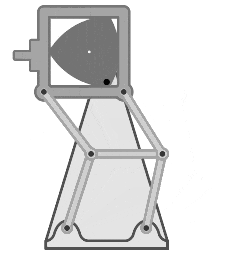
苏联 Luch-2 基于 Reuleaux 三角形的 8 毫米胶片放映机中的进片机构。丨图源：Reuleaux triangle - Wikipedia

Reuleaux 三角形的其它应用包括吉他拨片、消防栓防篡改螺母、铅笔形状的设计等等。

前文提及， 5 人团队在解决了 Schramm 问题后，就转向了离散几何的其它领域，但他们留下了一个新的高维几何世界供其他人探索。

2008 年，Schramm 在许多不同的数学领域取得了重大进展后，却在一次徒步旅行事故中丧生。作为他曾经的老师，Kalai 教授很高兴看到今天的研究者继承并延续了 Schramm 的学术遗产，结出丰硕的果实。

他说，以前在更高的维度中，人们都认为定宽体应表现得像球，至少在体积特性方面是这样，但“事实并非如此，所以这意味着高维几何体的理论非常丰富。”

2010 年，Gil Kalai 在 MathOverflow 上发帖，希望让更多数学家去关注那个“非常基本的问题”——Schramm 问题。

在今年 5 月最后的一天，Kalai 在这尘封已久的帖子下回复自己道：“问题已获解决。”